M203 20251220 Polynomials
1. Basic Polynomial Review
degree of polynomials

1 . Let $f(x) = 2x^2 + 5x + 13$ and $g(x) = x^3 - 3x - 4$. For what value of $c$ does the degree of $xf(x) + c \cdot g(x)$ equal $2$?
2 . Prove that if $f$ and $g$ are nonzero polynomials, then $\deg(f \cdot g) = \deg(f) + \deg(g)$.

7 . Find the degree of $f(g(x))$ given that $f$ and $g$ are polynomials such that the degree of $f$ is $m$ and the degree of $g$ is $n$, where $m$ and $n$ are nonnegative integers.
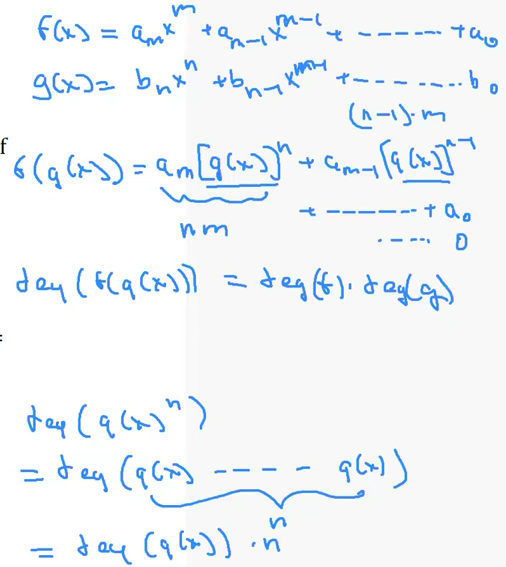
5) Let $f(x) = x^4 + x^2 - 2$ and $g(x) = 2x^3 + 3x^2 + 4x + 5$.
Find the degree of $f(g(x))$.
Find the degree of $f(f(f(f(x))))$.
Find the sum of the coefficients in the expansion of $g(f(x))$.
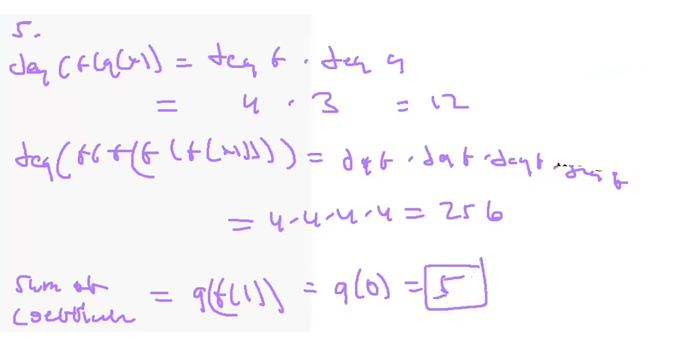
2. Polynomial Division
1) Suppose that $a$, $b$ and $c$ are constants such that
$(2x^2+3x+7)(ax^2+bx+c)=2x^4+11x^3+9x^2+13x-35$, find $a$, $b$, $c$.
2) Given $(x-5)g(x) = x^3 + 7x^2 - x + 11$, find $g(x)$.

3) Find the quotient and remainder for each of the following polynomial divisions:
b) $3x^4 + 13x^2 - 9x + 122$ divided by $x^2 + x + 4$
d) $19x^5$ divided by $x - 1$

3. The Remainder Theory
Remainder Theorem
Suppose $p(x)$ is divided by $(x-a)$ with remainder $r$. Then $r = p(a)$.
1) Let $f(x) = x^{10} - 2x^5 + 3$. Find the remainder when $f(x)$ is divided by $x - 2$.
2 ) Let $P(x)$ be a polynomial such that when $P(x)$ is divided by $x-19$, the remainder is $99$. And when $P(x)$ is divided by $x-99$, the remainder is $19$. Find the remainder when $P(x)$ is divided by $(x-19)(x-99)$.

| Degree of Divisor D(x) | Assumed Form of Remainder R(x) | Example |
|---|---|---|
| Degree 1 (e.g., $x-c$) | Constant $k$ | $R(x) = k$ |
| Degree 2 (Linear) | Linear Expression $ax+b$ | $R(x) = ax+b$ |
| Degree 3 (Quadratic) | Quadratic Expression $ax^2+bx+c$ | $R(x) = ax^2+bx+c$ |
3) Find the remainder when the polynomial $x^{81} + x^{49} + x^{25} + x^9 + x$ is divided by $x^3 – x$.
5 ) Find the remainder when $x^{100}$ is divided by $(x-1)(x-2)$.
4. The Factor Theorem
Let the polynomial $f(x)$ has the roots $r_1, r_2, r_3, \dots, r_n$. Then we can write $f(x)$ as
$f(x) = a(x - r_1)(x - r_2) \dots (x - r_n)$
1 ) Let $f(x)=6x^3-tx^2+7x-12$, where $t$ is a constant such that $f(x)$ is divisible by $x-2$. Find $t$.
3 ) The polynomial $f(x)=x^4+ax^3+bx^2+cx+d$ has roots $1,3,5$ and $7$. Determine sum of the coefficients of $f(x)$.
7 ) The polynomial $p(x)=3x^3 – 20x^2 + kx + 12$ is divisible by $x-3$ for some constant $k$. Factor $p(x)$ completely.
5. Vieta’s Formulas
设 $f(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_1 x + a_0$,并设 $f(x)$ 的根为 $r_1, r_2, \dots, r_n$。则有:
$$
\begin{aligned}
s_1 &= r_1 + r_2 + r_3 + \cdots + r_n &= -\frac{a_{n-1}}{a_n} \\
s_2 &= r_1 r_2 + r_1 r_3 + r_1 r_4 + \cdots + r_{n-1} r_n &= \frac{a_{n-2}}{a_n} \\
s_3 &= r_1 r_2 r_3 + r_1 r_2 r_4 + \cdots + r_{n-2} r_{n-1} r_n &= -\frac{a_{n-3}}{a_n} \\
&\vdots \\
s_n &= r_1 r_2 r_3 \cdots r_n &= (-1)^n \frac{a_0}{a_n}
\end{aligned}
$$
其中每个 $s_k$ 是 $f(x)$ 的根每次取 $k$ 个的对称和 (symmetric sum)。我们称这些方程为韦达定理 (Vieta's Formulas)。
3 ) Let $r$, $s$ and $t$ be the solutions to the equation
$3x^3 – 4x^2 + 5x + 7 = 0$.
Find $r+s+t$; Find $r^2+s^2+t^2$. Find $\dfrac{1}{r} + \dfrac{1}{s} + \dfrac{1}{t}$.
1) $f(x) = x^3 – 4x^2 + 15x – 7$, let $p$, $q$, $r$ be the roots of $f(x)$.
Find $pq+pr+qr$.
Find $pqr$.
---
2) Let $p$, $q$, $r$ and $s$ be the roots of $f(x) = 3x^4 + 2x^3 – 7x^2 + 9x - 10$.
Find $pqr + pqs + prs + qrs$.
4) One of the roots of $x^3 + ax + b = 0$ is $1+2i$, where $a$ and $b$ are real numbers. Find $a$ and $b$.
Here is the English explanation for why $1-2i$ must be a root of the equation.
The Complex Conjugate Root Theorem
This rule is known as the Complex Conjugate Root Theorem. It states that if a polynomial equation has purely real coefficients, any non-real complex roots must arrive in "conjugate pairs."
1. The Core Logic
For a polynomial $f(x) = x^3 + ax + b = 0$, where $a$ and $b$ are real numbers, if a complex number $z = 1+2i$ is a root, then its conjugate $\bar{z} = 1-2i$ must also be a root.
Mathematically, this is because the operation of taking a conjugate commutes with addition and multiplication. If $f(z) = 0$, then:
$$\overline{f(z)} = \overline{0} \implies f(\bar{z}) = 0$$
(This only holds true if the coefficients of the polynomial are unaffected by the conjugate operation—meaning they are real.)
---
2. Intuitive Understanding
- Geometric Symmetry: On the Complex Plane (Argand diagram), the numbers $1+2i$ and $1-2i$ are reflections of each other across the horizontal real axis.
- Canceling the Imaginary Parts: The right side of your equation is $0$, which is a real number. When you plug $1+2i$ into $x^3 + ax + b$, it generates complex terms. To "cancel out" these imaginary $i$ components and return to a result of zero, there must be a "partner" root ($1-2i$) that provides the exact opposite imaginary values.
- Constructing Real Coefficients: When you multiply the factors $(x - (1+2i))$ and $(x - (1-2i))$ together, the $i$ terms disappear:
$$(x-1-2i)(x-1+2i) = (x-1)^2 + 4 = x^2 - 2x + 5$$
Notice how the resulting quadratic has only real coefficients ($1, -2, 5$). If the partner $1-2i$ were missing, the final polynomial would inevitably contain $i$, which contradicts the fact that $a$ and $b$ are real.
---
3. Important Exception
If the coefficients $a$ or $b$ were complex numbers (e.g., $a = 3i$), this symmetry breaks down. In that case, $1-2i$ would not necessarily be a root because the "imbalance" is already built into the equation itself.
5) Evaluate $(2-r)(2-s)(2-t)$ if $r,s,t$ are the roots of $f(x) = 2x^3 - 4x^2 + 3x - 9$.
11) Find $(2+r)(2+s)(2+t)(2+u)$ if $r$, $s$, $t$ and $u$ are the roots of $f(x) = 3x^4 - x^3 + 2x^2 + 7x + 2$.